Twenty Three Hundred
Digital Logic
Dr Charles Martin
Semester 1, 2022
Week 1: Boolean algebra
George Boole
It starts with a thought
An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities by George Boole, 1854
You can still buy it from Amazon
Boole’s big idea: true & false are all you need
What is Boolean algebra?
Algebra is the study of mathematical symbols and the rules for manipulating these symbols; it’s about variables like a and b and operators like ∧ (binary and), ∨ (binary or), ¬ (unary not, sometimes represented with an overline e.g. $\overline{q}$).
Boolean means that all variables & expressions can take one of two values. We can call them true and false, 1 and 0, or Mary and Mengyuan; it doesn’t matter.
Boolean algebra builds expressions with these basic building blocks, e.g.
¬(a ∧ b) ∨ c
this is all revision from MATH1005, so we’re gonna speed through
Truth tables
Truth tables are just a convenient way of enumerating all the of the possible values our variables can take. If you’ve got $n$ variables, you need $2^n$ rows in your truth table (why?)
Here’s an example with 2 variables:
| a | b | a∧b |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Other handy Boolean operators
| a → b = (¬a ∨ b) | a implies b |
| (a ≡ b) = (a ∧ b) ∨ (¬a ∧ ¬b) | a equivalent to b |
| (a ⊕ b) = (a ∧ ¬b) ∨ (¬a ∧ b) | a exclusive or/xor b |
| ¬(a ∧ b) = (¬a ∨ ¬b) | a not and/nand b |
| ¬(a ∨ b) = (¬a ∧ ¬b) | a not or/nor b |
You can reduce any Boolean expression to only NAND or only NOR operators (try it and see!).
Logic functions
You know about functions from maths, e.g. here’s a two-argument function of $x, y \in \mathbf{R}$
$f(x, y) = x^2sin(y)$
We can have functions of Boolean variables $a$ and $b$ as well:
$g(a, b) = \ldots$
talk
$f(x, y) = \ldots$
$g(a, b) = \ldots$
Can you think of anything we can do with the Boolean function $g(a,b)$ that we can’t do with the real-valued function $f(x,y)$?
Full binary operator truth table
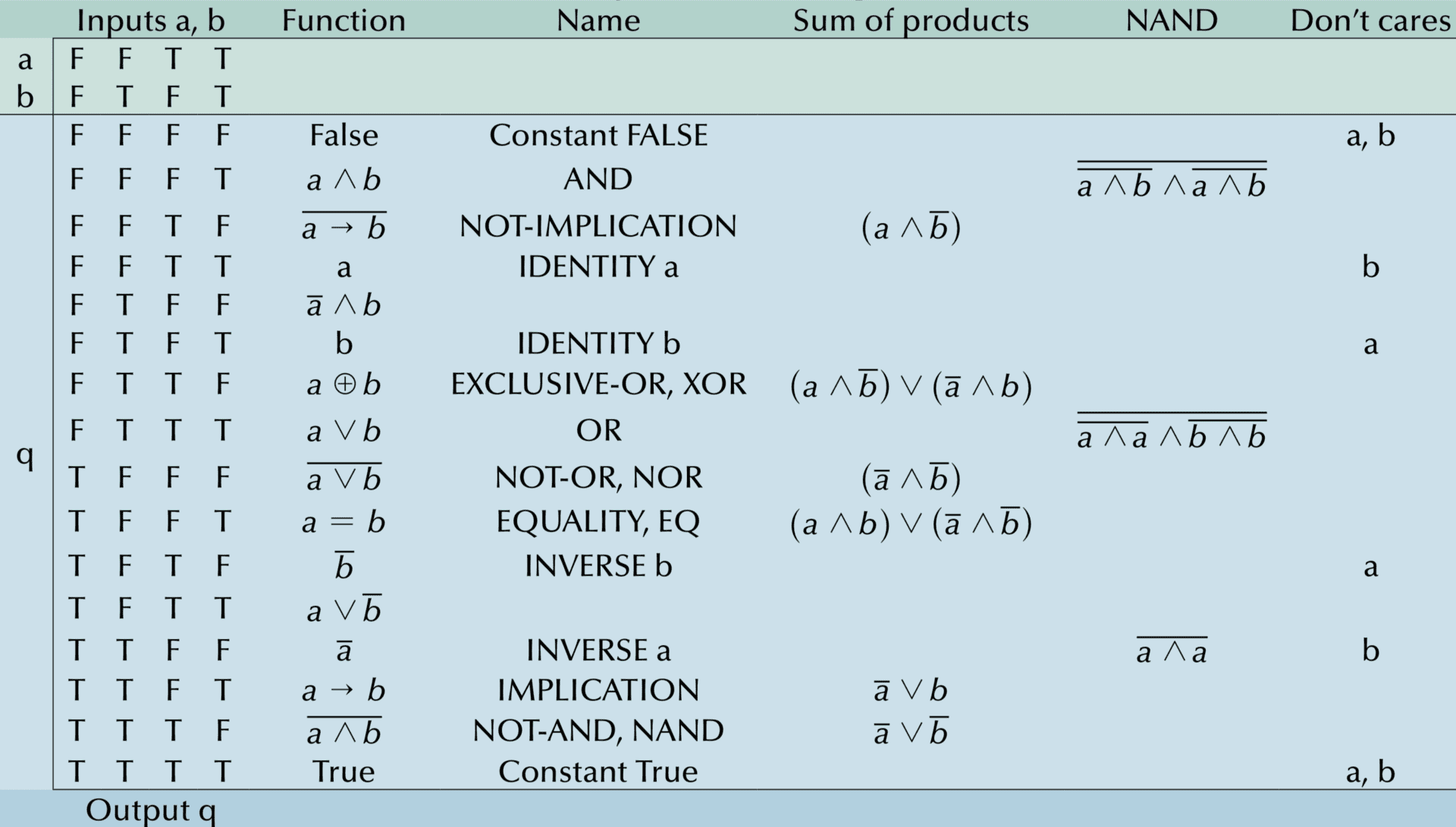
What does this have to do with my microbit?
Logic gates
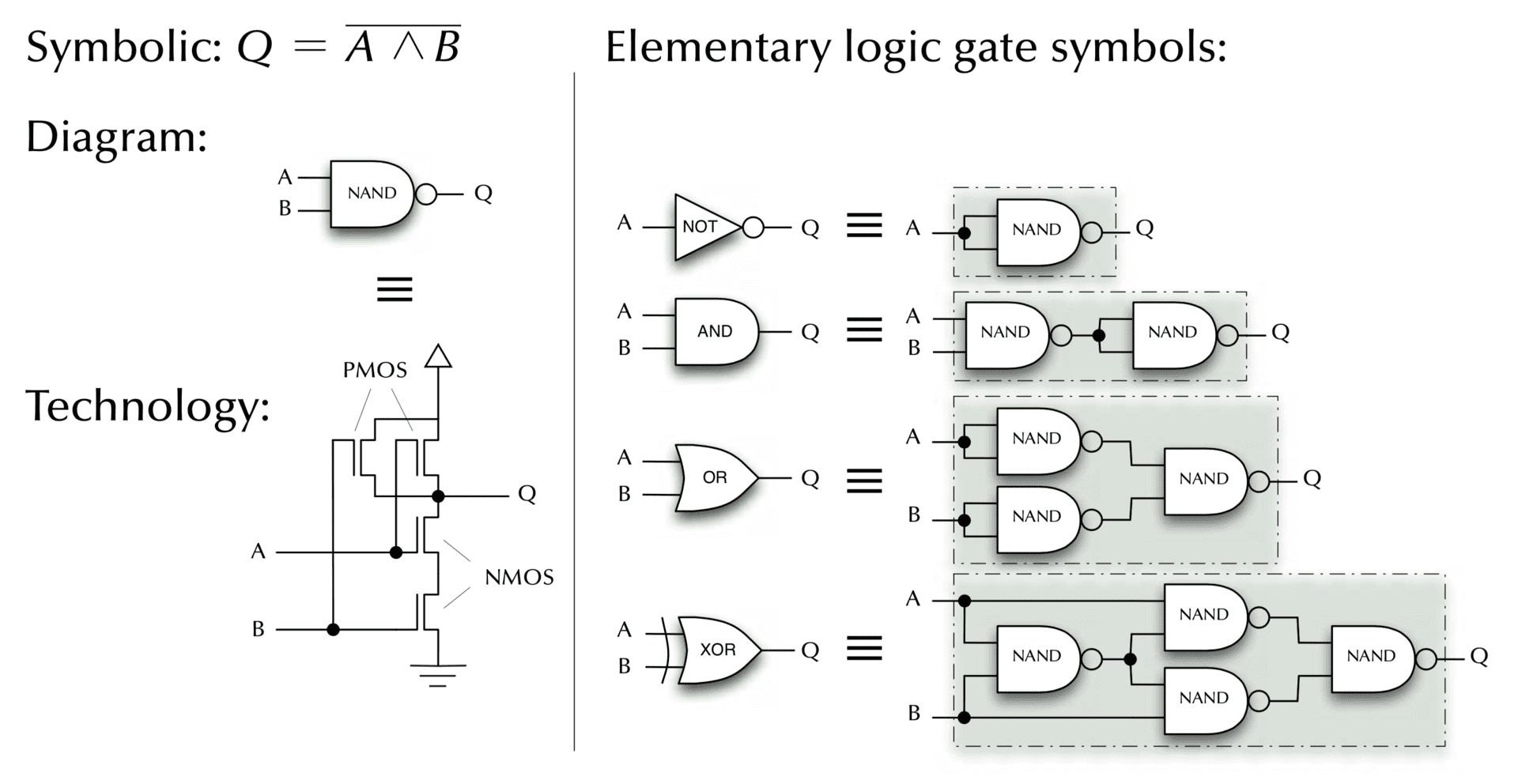
How does your computer add 1+1?
How would a 5yo do it?
Number representations
Remember that an integer can be represented in a different “base” (or “radix”), e.g. binary (base-2), octal (base-8), hexadecimal (base-16) or the familiar decimal (base-10).
| Decimal | |
| Hex | |
| Binary |
Note: hex & binary padded to 32-bit, negative numbers represented with 32-bit two’s complement
Combinational logic
Let’s start simple: 1+1
Consider the Boolean function $s(a, b) = a + b$ (the s is short for sum). How would we put this in a (pseudo) truth table?
| a | b | s |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 2 |
Not quite…
This doesn’t really work because we can’t have three distinct values (0, 1 and 2) in Boolean algebra. But what if we just consider one “column” of the addition?
| a | b | s | |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | (carry the 1) |
Add a c (carry) column
| a | b | s | c |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
bit == binary digit
But what is $s(a,b)$?
The truth table is a complete spec for the function $s(a, b)$ that we’re interested in, but it doesn’t tell us how to express $s$ using the rules we looked at earlier.
| a | b | s | c | s minterms | c minterms |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | ||
| 0 | 1 | 1 | 0 | ¬a ∧ b | |
| 1 | 0 | 1 | 0 | a ∧ ¬b | |
| 1 | 1 | 0 | 1 | a ∧ b |
s = (a ∧ ¬b) ∨ (¬a ∧ b) = a ⊕ b
c = a ∧ b
So far...
Combinational Logic:
lets us make a Boolean expressions for any truth-table
Boolean Algebra:
lets us simplify Boolean expressions to something manageable
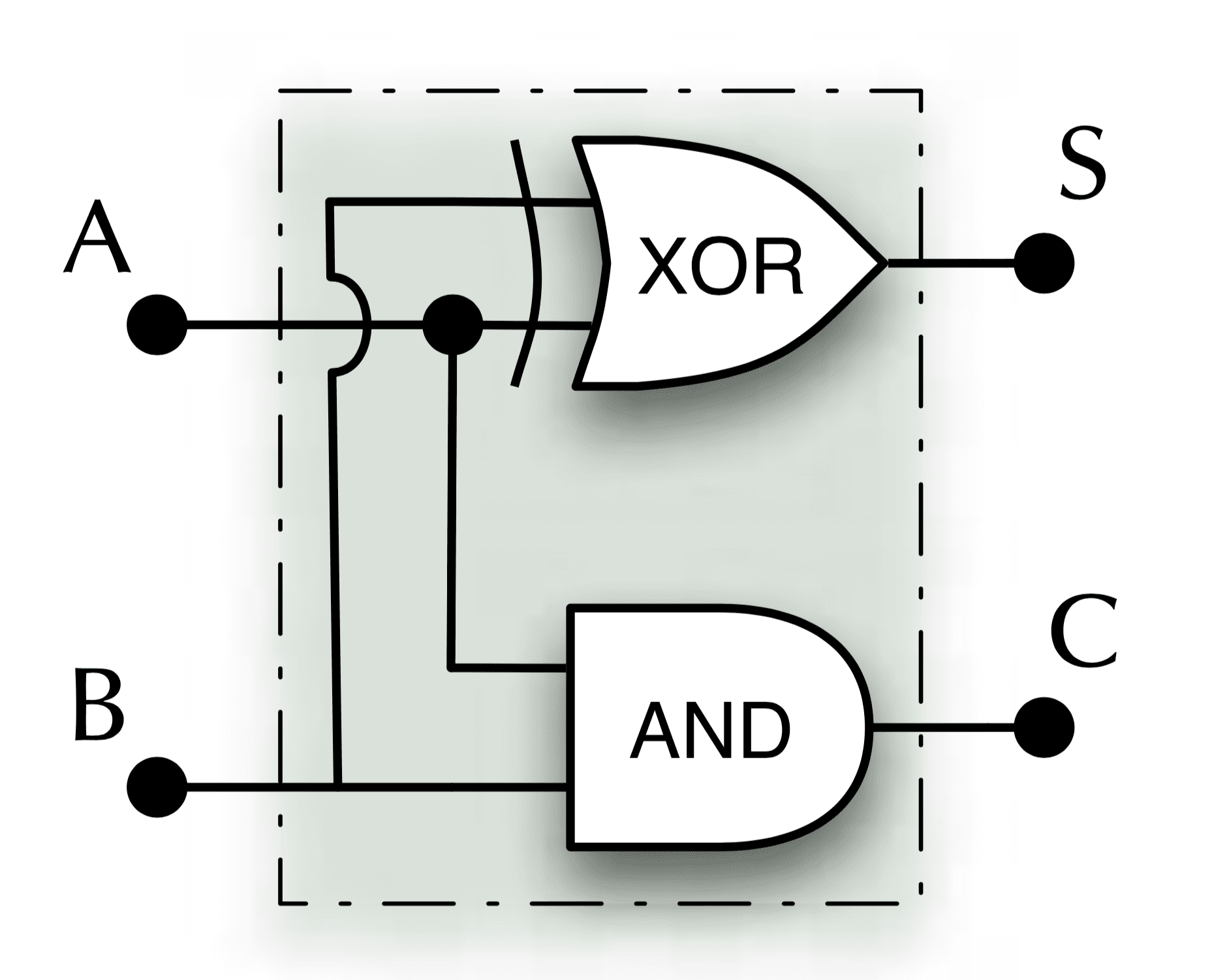
Half-adder
s = a ⊕ b
c = a ∧ b
DLS: Digital Logic Simulator
DLS is a time-driven event-based multi-delay 3-value digital logic simulator.
There’s both desktop (cheap) & web (free) versions.
DLS isn’t compulsory for the course, but it’s a nice way for me to demo things.
Demo: Half-adder
Full-Adder
What about carry in?
What’s missing with the half-adder? Carry in (ci) as well as carry out (co).
| a | b | ci | s | co |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
s = (a ∧ ¬b ∧ ¬ci) ∨ (¬a ∧ b ∧ ¬ci) ∨ (¬a ∧ ¬b ∧ ci) ∨ (a ∧ b ∧ ci)
= (((a ∧ ¬b) ∨ (¬a ∧ b)) ∧ ¬ci) ∨ (((¬a ∧ ¬b) ∨ (a ∧ b)) ∧ ci)
= ((a ⊕ b) ∧ ¬ci) ∨ ((a = b) ∧ ci)
= ((a ⊕ b) ∧ ¬ci) ∨ (¬(a ⊕ b) ∧ ci)
= (a ⊕ b) ⊕ ci
Full-adder
cout = (a ∧ b) ∨ ((a ⊕ b) ∧ cin) (trust me!)
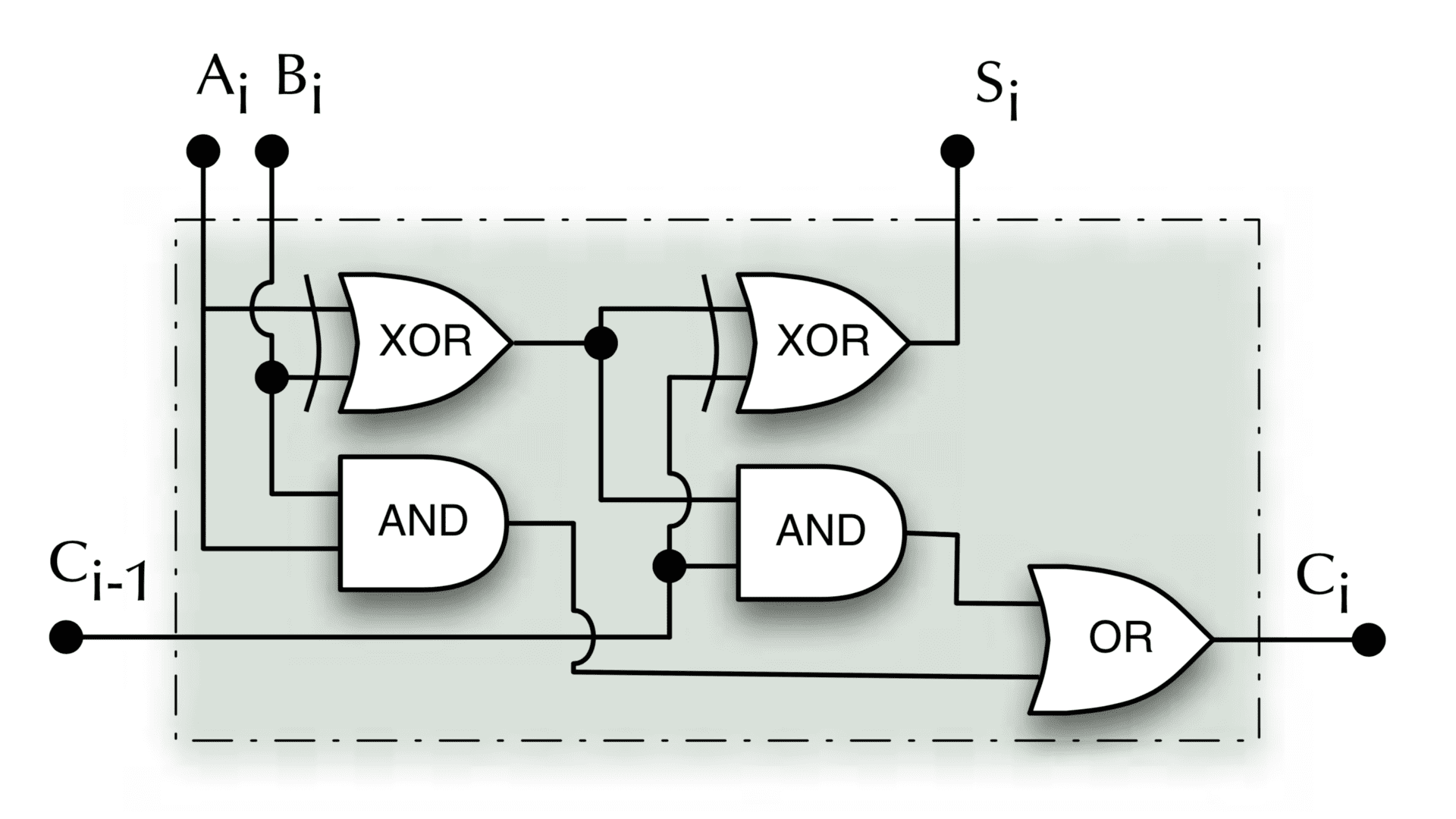
Demo: Full-adder
Ripple-carry adder
We can join them together like so:
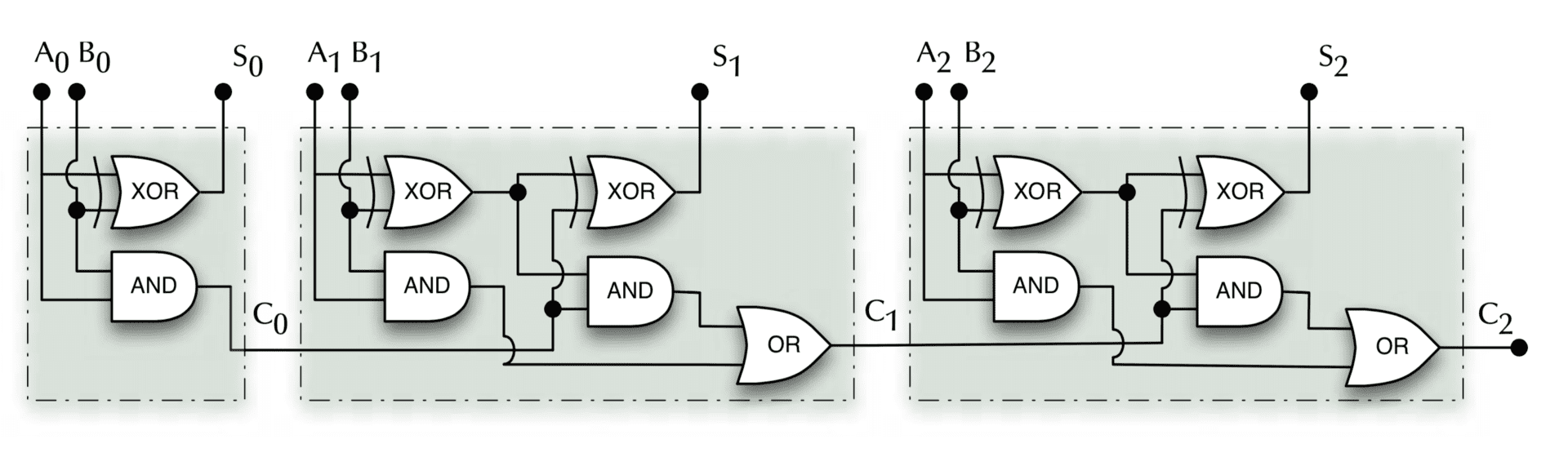
talk
- how many bits can be added together?
- how long does it take?
- where does the final carry bit go?

What about subtraction?
We’ve got two options:
- do some more minterms stuff (boo!)
- trick the full adder into subtracting things instead
show of hands?
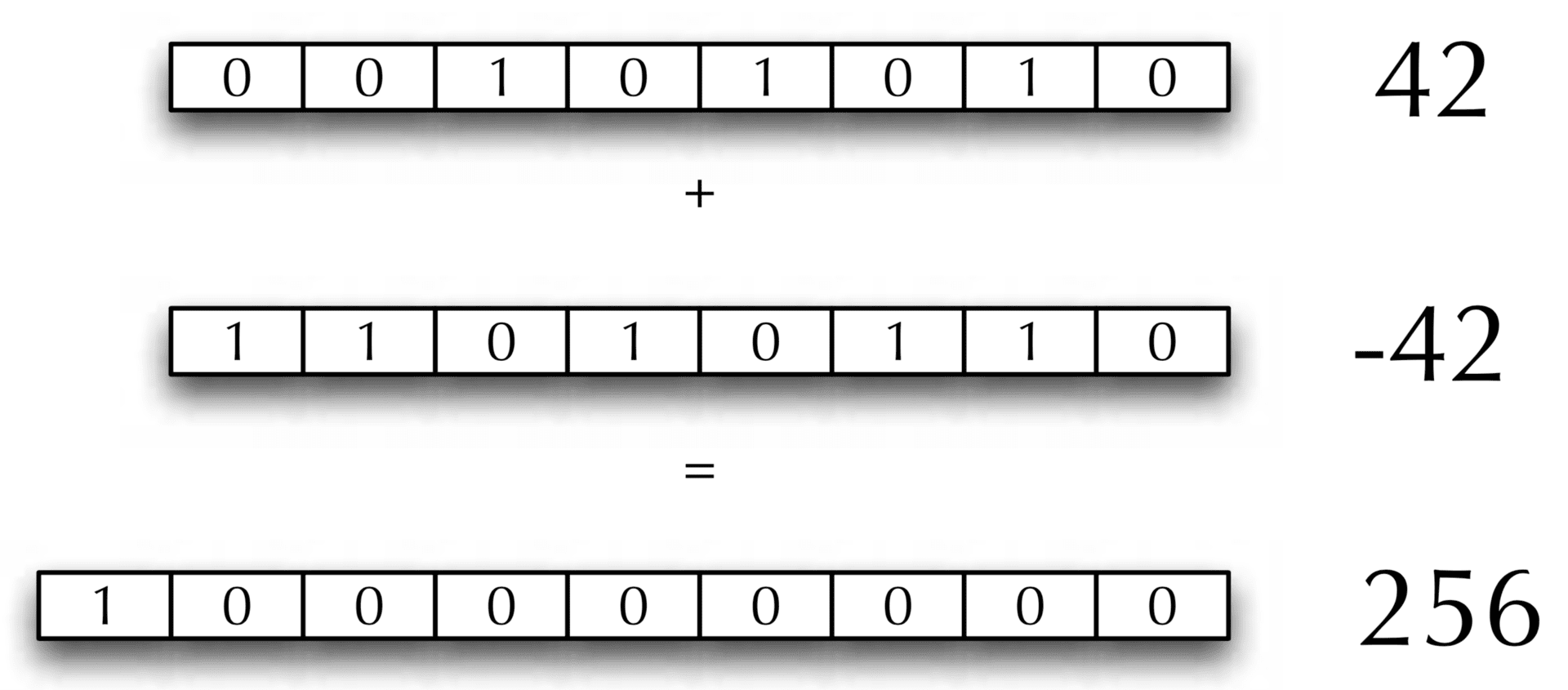
Twos complement representation
The basic idea: can we define (binary) negative numbers such that our adder still works?
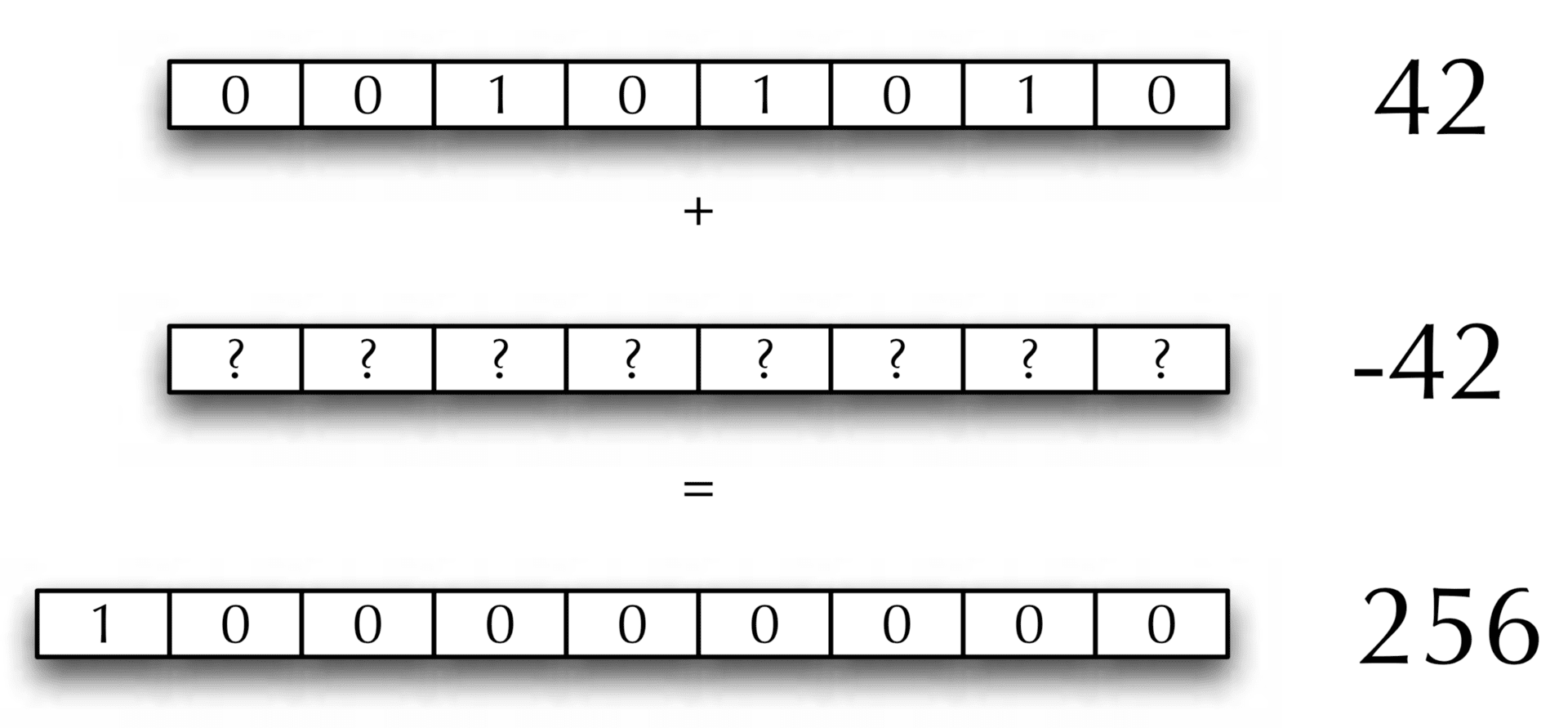
Twos complement representation
also remember the number conversion widget from earlier
The twos complement “circle”

Quiz: negative or positive?
0b10
0b011011
0b011011101110101010010
0b1011000000000011101111111111101010010000000001010101
it’s all in your mind
Simple ALU
A simple ALU (Arithmetic & Logic Unit) which can ADD, XOR, AND, OR two arguments.
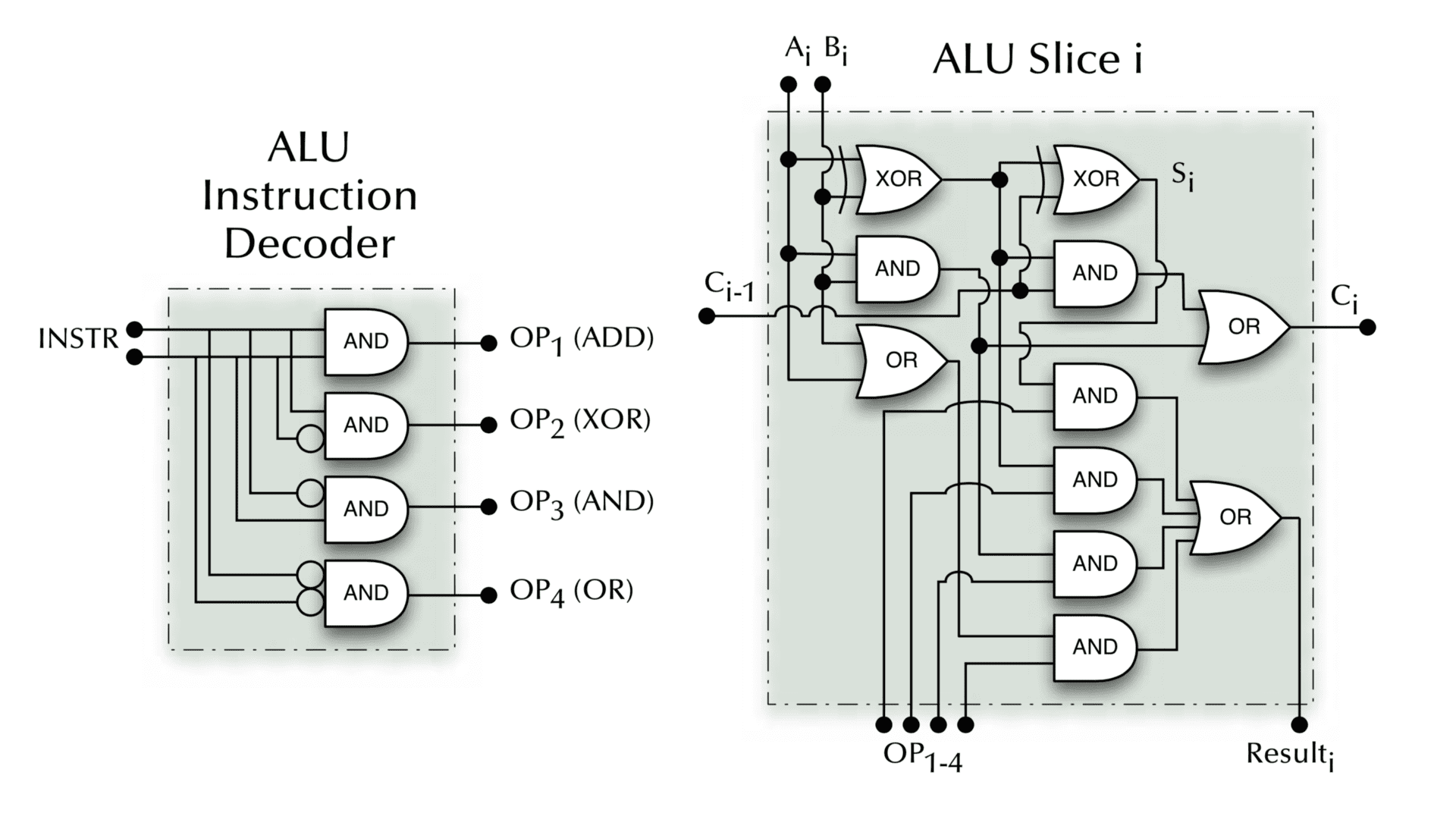
Sequential logic
talk
What does it mean for a computer to have memory? Can the combinational logic functions we’ve looked at so far remember things?
no! we need feedback
Sequential == state-oriented
This makes intuitive sense—the feedback loop allows the current output to be fed back in (as input).
Sequential logic circuits can no longer be treated as “pure” input-output black boxes—they carry “state” (i.e. the sequence of inputs matters).
SR latch
S (set), R (reset)
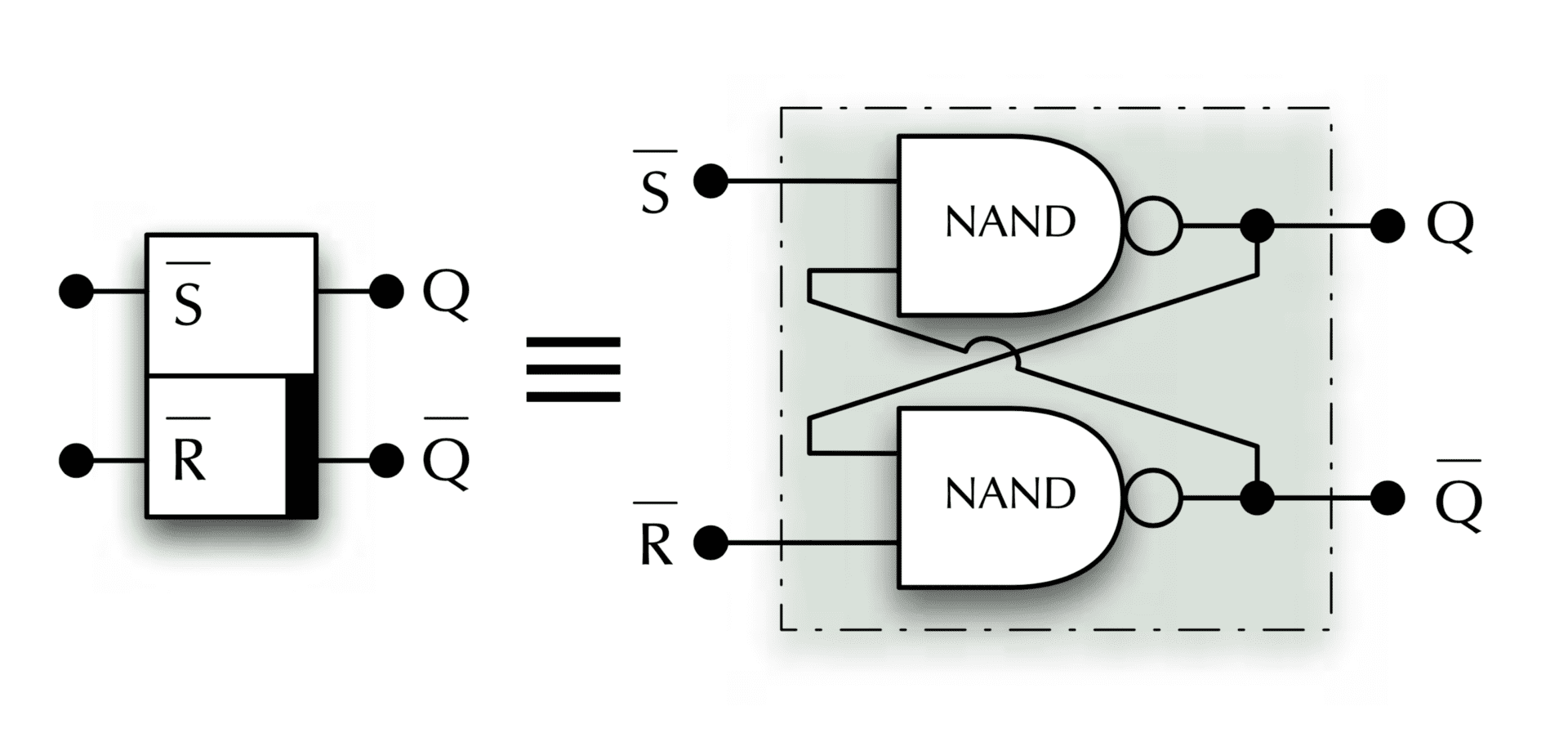
stackexchange asks: “Why is the output of stateful elements often named Q?”
SR input
There are four possible input combinations:
| ¬s | ¬r | effect |
|---|---|---|
| 1 | 1 | keep current state q |
| 0 | 1 | set q (to 1) |
| 1 | 0 | reset q (to 0) |
| 0 | 0 | forbidden (q and ¬q both set to 1) |
Demo: SR latch
Problems with the SR latch
- the forbidden thing (this is obviously bad)
- there are some tricky timing issues (because physics: remember, there are real electrons flying around)
- have to keep changing inputs…
Gated D latch
The gated D latch uses an enable input, so that the latch is set only when you want it to be.
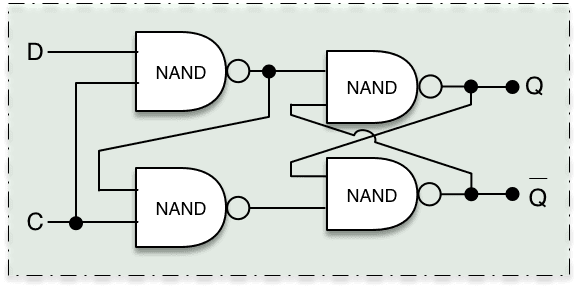
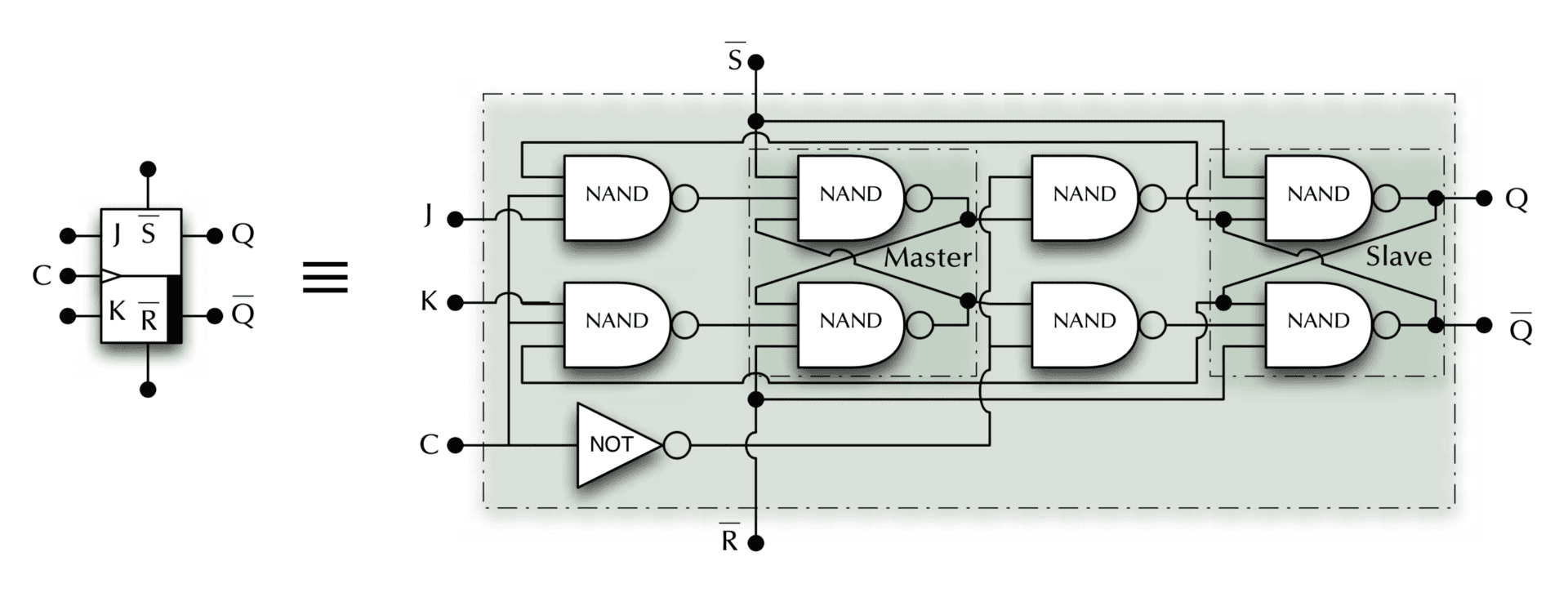
JK master-slave flip-flop
Better again, set/reset on a clock: no timing problems, no forbidden inputs, toggle operation (although it’s a more complex circuit)
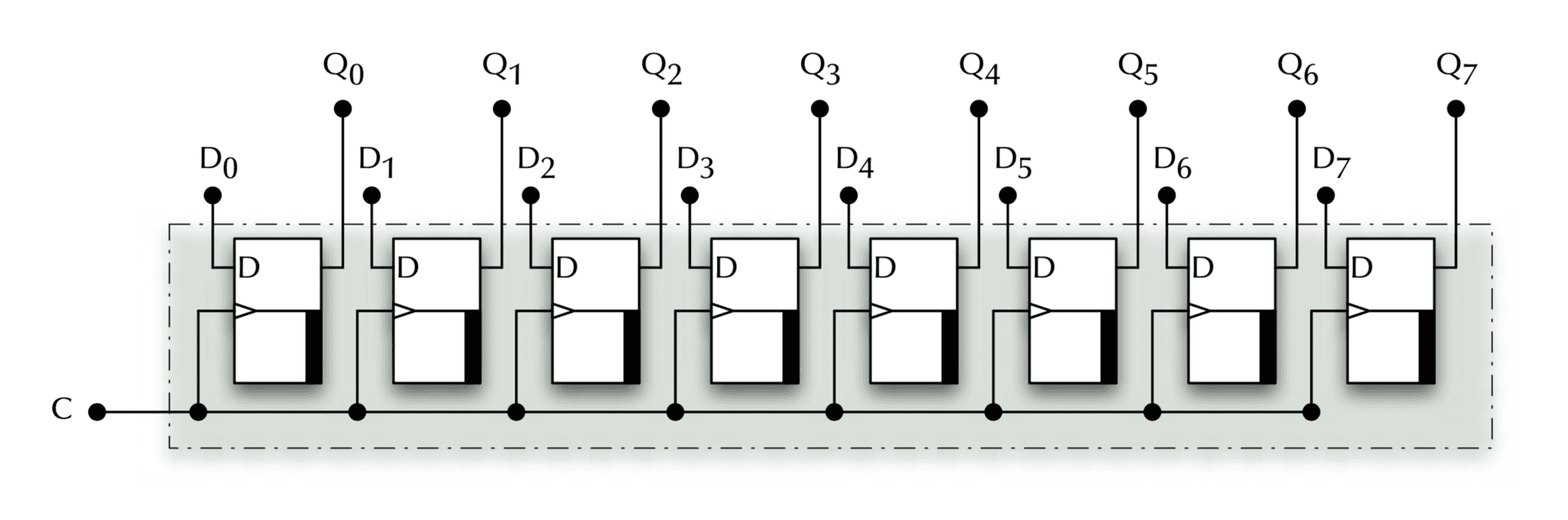
Register
Store multiple bits, can serve as general-purpose fast on-CPU storage, or hold state for peripherals, etc. Note the shared clock line
Counter

Your microbit has several of these!
Feeling lost?
These are all physical components in your computer.
There’s no magic (!), just these billion of these little mathematical machines.
Further reading
Plantz: Introduction to Computer Organization chapters 5-7
Patterson & Hennessy Appendix A “The Basics of Logic Design”
EEVblog Intro to Digital Logic (YouTube)
Ben Eater: Logic Gates, SR Latch, D Latch, D Flip-Flop, JK Flip Flop